Удар

Удар. При встрече движущегося тела с каким-нибудь другим телом между ними происходит взаимодействие, называемое ударом. Прямая линия, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения, называется линией удара. Если линия удара проходит чрез центры тяжести обоих тел, то удар называется центральным; в противном случае он называется эксцентричным. Понятно, что удар между однородными шарами всегда будет центральным. Если до удара оба тела двигались по линии удара, удар называется прямым; в противном случае — косым. Положим, что два тела I и II движутся в одну сторону по линии, соединяющей их центры тяжести, со скоростями v₁ и v₂, причем v₁>v₂, так что I тело догонит и ударит II (из условия видно, что удар будет прямой центральный). С этого момента, в течение некоторого промежутка времени¹⁾, оба тела будут давить друг на друга по линии удара с силами равными и противоположными.

¹⁾ Длительность этого промежутка зависит от размеров и вещества соударяющихся тел, а также от их скорости. При соударении стальных или медных шаров радиусом в 1 дм, двигающихся с относительной скоростью 1 фт/сек, продолжительность удара несколько более 0,0001 сек. Вообще, в обычных опытах удар бывает очень кратковременным явлением; а так как за время удара скорости сталкивающихся тел претерпевают значительные изменения, то очевидно, что силы, производящие это изменение скоростей, должны быть весьма значительны, но действовать в течение малых промежутков времени (т. н. мгновенные силы). Однако, если бы столкнулись два стальных шара, имеющие размеры земли и двигающиеся с относительной скоростью 1 см/сек, то длительность удара составила бы более, чем сутки.

Говоря об ударе, подразумевают всегда тела, способные к изменению формы; итак, вышеуказанные силы произведут изменение формы («деформацию»), а именно сплющение рассматриваемых тел. Кроме того, они будут изменять скорости тел: скорость v₂ будет увеличиваться, а v₁ уменьшаться. Так как явление, очевидно, сохраняет этот характер все время, покамест v₁> v₂, то, понятно, должно наступить равенство: v₁ = v₂. В этот момент заканчивается первая стадия удара. Затем мыслимы 3 случая, в зависимости от вещества соударяющихся тел: 1) или никаких дальнейших изменений скорости тел не происходит; тела движутся дальше вместе, с одинаковой скоростью, как одно тело, и сохраняют полученную деформацию. В этом случае тела называются вполне неупругими (у других авторов — совершенно мягкими); 2) или, получив одинаковые скорости, тела начинают разжиматься под действием упругих сил, стремящихся восстановить прежнюю форму тел. При этом каждое тело продолжает давить на другое тело, и, следовательно, v₁ еще уменьшается, а v₂ увеличивается; таким образом, становится v₁ < v₂. В конце концов, вполне восстанавливается та форма тел, которая была до удара, и этим заканчивается вторая и последняя стадия удара. Такие тела называются вполне упругими. Наконец, 3-й случай отличается от 2-го тем, что прежняя форма тел не вполне восстанавливается. Такие тела зовутся телами средней упругости. Все тела природы принадлежат именно к этому последнему типу. 1 и 2 тип — лишь результаты абстракции. Однако опыт показывает, что, например, слоновая кость и сталь близко подходят к телам, обладающим совершенной упругостью, а свинец — к телам вполне неупругим. На основании теорем динамики можно доказать, что в случае прямого центрального удара упругих тел относительная скорость I тела по отношению к II не меняет своей величины, а меняет только знак (частные случаи: если массы обоих тех равны, то каждое тело после столкновения будет иметь ту скорость, какую имело другое тело до столкновения; если тело ударяется о неподвижную стену, то оно отскакивает с той же величиной скорости в противоположную сторону). Если сталкивающиеся тела не упруги, то относительная скорость после удара обращается в нуль. Ньютон предположил, что в случае тел средней упругости относительная скорость тел после удара составляет только некоторую долю (k) той относительной скорости, которая была до удара, и, кроме того, меняет знак; k называется коэффициентом восстановления; для тел вполне упругих k=1, а для вполне не  упругих k=0. Отсюда выводится следующее выражение потери живой силы при ударе:

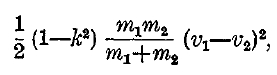
где m₁ и m₂ — массы обоих тел, v₁ и v₂ — их скорости до удара (потерянная живая сила идет на деформацию тел и на их нагревание). Интересно применить эту формулу, например, к столкновению гвоздя и молотка. Пусть буквы с значками 1 относятся к молотку, а с значками 2 — к гвоздю. Тогда v₂=0; живая сила до удара выразится ½ m₁v₁² отношение потери живой силы ко всей живой силе будет (1-k²)m₂/(m₁+m₂) сделать это отношение возможно малым, нужно увеличить m₁ по сравнению с m₂; таким образом, при одной и той же живой силе, сообщаемой молотку, выгоднее пользоваться тяжелым молотком при меньшей скорости, чем легким молотком при большей скорости. Слишком легкий молоток будет сильно деформировать гвоздь. В более общем смысле ударом называют всякое резкое изменение связей какой-нибудь системы; так, например, если тело, к которому привязана нить, летит в воздухе, и мы, хватая за эту нить, натягиваем ее, то тело подвергается удару. Если мы заставляем камень, привязанный к нити, описывать окружность около руки, держащей конец нити, и если нить обрывается, то камень также испытывает удар.

А. Бачинский.